Czworokątne pole otoczone jest rowem jednakowej wszędzie szerokości. Do rozporządzenia są dwie deski, których długość zrówna się dokładnie szerokości rowu. Należy za pomocą tych desek zbudować przejście przez rów.

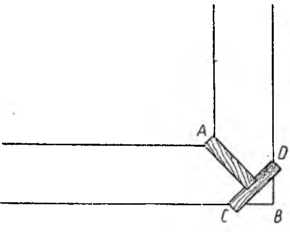Figura daje poglądowe rozwiązanie zadania.
Matematyczny dowód możliwości podanej przeprawy wynika z nierówności   √2 < 1 ½.

Jeżeli za jednostkę długości przyjmiemy szerokość rowu, to odległość AB wyrazi się liczbą √2, czyli około 1,414. Długość deski jest dokładnie równa szerokości rowu, a więc wyraża się liczbą 1. Gdy przy rogu B położymy jedną deskę na ukos, utworzy się trójkąt prostokątny równoramienny BCD i brzeg deski CD będzie od rogu A odległy o √2 — czyli o 0,914 jednostki długości. Stąd wniosek, że można na tej desce ułożyć drugą deskę sięgającą rogu A i na oparcie tej deski po obu jej końcach zostanie jeszcze 0,086 jednostki długości (np. przy deskach trzymetrowych zostanie ponad 25 cm).