Aby ziemniaki wydały maksimum plonu, należy je sadzić w pewnej stałej odległości przepisanej przez naukę opartą na wieloletnim doświadczeniu. Chodzi jednak o to, jakie będzie najkorzystniejsze ich rozmieszczenie na polu. I w tej sprawie ma coś do powiedzenia nie tylko agronomia, lecz i matematyka.

Jak wiadomo, istnieją trzy takie wielokąty, na które można rozbić bez przerw i luk płaszczyznę, mianowicie: trójkąt równoboczny, kwadrat i sześciokąt foremny. Tylko więc te trzy rodzaje wzajemnego rozmieszczenia ziemniaków można brać pod uwagę. Że przy stosowaniu sześciokąta (wobec koniecznego stałego minimum odległości między ziemniakami) gleba nie będzie dostatecznie wyzyskana, to jest prawie oczywiste. Wątpliwość może powstać tylko przy wyborze trójkąta lub kwadratu. W każdym z tych wielokątów umieścimy pośrodku jedną roślinę, przy czym dobierzemy wymiary prostokątów w taki sposób, by odległość między najbliższymi siebie roślinami miała przepisową wielkość, np. d — 56 cm. (Gdyby ktoś chciał przeprowadzić obliczenia dla innej wartości d, nie będzie miał większego kłopotu).

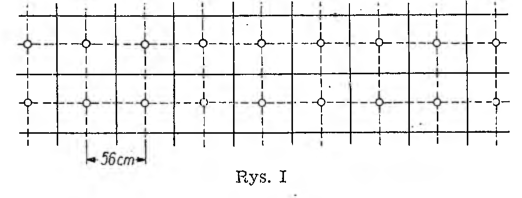Przy sadzeniu ziemniaków w „kwadrat”, jak pokazuje rysunek I, musimy rozmieścić rzędy w odstępach po 56 cm i w każdym rzędzie sadzić rośliny co 56 cm. Na każdą roślinę przypadnie 56 • 56 = 3136cm² gruntu, a na jednym arze (10X10 m) posadzimy 1 000 000 : 3136 = 319 roślin.

Rozważmy jeszcze sposób sadzenia ziemniaków w wierzchołkach trójkątów równobocznych (rys. II).

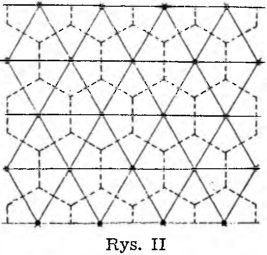Przy tym sposobie sadzenia na każdą roślinę przypadnie sześciokąt foremny, w którym odległość środka od boków wynosić będzie 28 cm. Cały ów sześciokąt foremny można rozbić na 6 trójkątów równobocznych.

W każdym z tych trójkątów wysokość wynosi 28 cm, a bok — jak łatwo obliczyć — około 32 cm. Pole takiego małego trójkąta wynosi ½ • 32 • 28 = 448 cm², a pole całego sześciokąta foremnego zajmuje 6 • 448 = 2688 cm². Na jednym arze można wysadzić 1 000 000 : 2688 = 372 rośliny, czyli więcej niż przy sadzeniu w kwadrat.