Mnożenie na palcach

Przy omawianiu dziwów dziewiątki przytoczyliśmy znakomity sposób palcowego mnożenia przez tę liczbę.

Pewien autor syryjski z XVII w., nazwiskiem Beha-Eddin (1547-1622), w dziełku swym bardzo rozpowszechnionym w Persji i Indiach pod tytułem Khelasat as hissab (O istocie rachunków) podaje odmienny nieco, ale równie pomysłowy sposób palcowego mnożenia przez inne liczby, niezbędny dla tych, co nie chcą lub nie mogą sięgać w nauce tabliczki mnożenia powyżej 5.

Kto zdobył tajemnicę, ile jest 2 • 2, 2 • 3 i tak dalej aż do 5 • 5, ten wyżej iść już w tej trudnej nauce nie potrzebuje, wystarczą mu bowiem do bardziej skomplikowanych mnożeń palce.

Przypuśćmy, że trzeba wykonać mnożenie 9 • 8.

Ale 9 = 5 + 4, a 8 = 5 + 3, to znaczy
9 • 8 = (5 + 4) • (5 + 3).

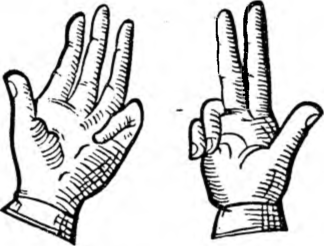Należy tedy podnieść 4 palce u jednej ręki i 3 palce u drugiej ręki. Suma palców podniesionych (4 + 3) wskaże liczbę dziesiątek iloczynu (7), a jedności iloczynu osiągniemy mnożąc liczbę zgiętych palców jednej ręki przez liczbę takichże palców drugiej ręki: 1 • 2 = 2.

A więc ostatecznie 9 • 8 = 72.

Przy mnożeniu 8 • 7, co daje (5 + 3) • (5 + 2), należy podnieść u jednej ręki 3 palce, a u drugiej 2 i pozostałe palce zgiąć. Suma wyprostowanych palców 3 + 2 = 5 będzie to liczba dziesiątek, a iloczyn zgiętych palców 2 • 3 = 6 będzie to liczba jedności poszukiwanego wyniku. Razem będzie 56. Taki to jest trudny przypadek mnożenia.

A jednak, .. . jednak chyba lepiej wyuczyć się po prostu tabliczki mnożenia.