Wśród figur „magicznych” cieszyły się i do dziś cieszą się największą wziętością kwadraty magiczne. Są to kwadraty rozbite na pewną ilość mniejszych kwadracików, czyli pól, w których liczby stanowiące pewien postęp wypisuje się w ten sposób, że suma liczb w każdym poziomym rzędzie i w każdej pionowej kolumnie, i na obu przekątnych jest zawsze jedna i ta sama.

Kwadraty magiczne znane były Chińczykom i Hindusom^ przed paru tysiącami lat. Spotyka się amulety chińskie z kwadratami magicznymi, na których jeszcze nie ma cyfr, lecz są odpowiednie ilości nakłuć lub wydrążeń. Znane one były również Arabom w IX wieku nowej ery. Do Europy zaś wprowadził je, a przynajmniej pierwsze prawidła ich zestawień wskazał Europejczykom pewien Grek imieniem Moscopulos, który żył w Konstantynopolu w początkach XV stulecia.

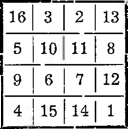Najbardziej historycznym kwadratem magicznym w Europie nazwać można bez wątpienia ten, który widnieje na jednym z arcydzieł pędzla D ii r e r a zatytułowanym Melancholia. Jest to kwadrat złożony z 16 pól, a zestawiony tak pomysłowo, że dwie środkowe liczby dolnego rzędu dają rok powstania dzieła:

1514

I wieki późniejsze, i czasy nowożytne nie przestały interesować się figurami magicznymi. Wielcy matematycy, a głównie matematycy francuscy, jak Bachet, Fre-nicle, Fermat, Poignard, La Hire, z zapałem opracowują przeróżne metody zestawiania magicznych kwadratów. Ozanam w swych Recreations poświęca im cały rozdział XII pierwszej części. B. Violle w roku 1837 wydaje trzytomowe dzieło poświęcone wyłącznie kwadratom magicznym pod tytułem Traite complet des ąuarres magiąues. Wreszcie M. A r n o u x w ciekawych studiach ogłoszonych w roku 1894, reasumując cały dorobek swych poprzedników, rzuca wiele nowego i ciekawego światła na to odwieczne zagadnienie.