 Dwaj bracia otrzymali w spadku po ojcu duży oparkaniony dookoła plac w kształcie trójkąta. Postanowili podzielić go na równe części po linii prostej tak, żeby na wspólnej granicy można było postawić jak najkrótszy parkan.
Dwaj bracia otrzymali w spadku po ojcu duży oparkaniony dookoła plac w kształcie trójkąta. Postanowili podzielić go na równe części po linii prostej tak, żeby na wspólnej granicy można było postawić jak najkrótszy parkan.
Niełatwą miał pracę mierniczy, do którego z takim zwrócili się żądaniem. Począł jednak przypominać sobie różne prawidła geometryczne i wreszcie odszukał miejsce, w którym należało pociągnąć granicę. Pójdźmy za jego rozumowaniem:
Ze wszystkich trójkątów o danej podstawie i danym kącie przy wierzchołku największe pole będzie miał trójkąt równoramienny, ponieważ geometrycznym miejscem wierzchołków takich trójkątów będzie łuk mieszczący dany kąt, a najwyższy punkt łuku leży w jego środku. Odwrotnie więc powiedzieć można, że ze wszystkich trójkątów mających dane pole i dany kąt u wierzchołka najmniejszą podstawę ma trójkąt równoramienny. Ze wszystkich zaś trójkątów równoramiennych mających dane pole ten będzie miał najmniejszą podstawę, którego kąt u wierzchołka będzie najmniejszy.
Z geometrii elementarnej wiadomo ponadto, że pola dwóch trójkątów mających jeden kąt wspólny mają się tak do siebie, jak iloczyny boków tworzących ów kąt wspólny.
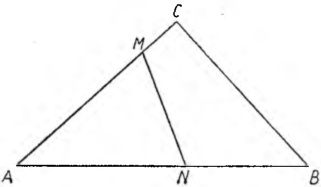 Na zasadzie powyższych przesłanek należało w trójkątnej parceli ABC (obacz rysunek) od wierzchołka A, którego kąt jest najmniejszy, odłożyć wzdłuż obu boków odcinki AM = AN równe średniej proporcjonalnej między jednym z boków AB lub AC i połową drugiego boku. Linia MN będzie linią poszukiwanej granicy, gdyż
Na zasadzie powyższych przesłanek należało w trójkątnej parceli ABC (obacz rysunek) od wierzchołka A, którego kąt jest najmniejszy, odłożyć wzdłuż obu boków odcinki AM = AN równe średniej proporcjonalnej między jednym z boków AB lub AC i połową drugiego boku. Linia MN będzie linią poszukiwanej granicy, gdyż
Δ AMN : Δ ABC = (AM • AN) : (AC • AB),
to znaczy
Δ AMN : Δ ABC = ½,
a więc trójkąt AMN stanowi połowę trójkąta ABC.