Linie arytmetyczne
Zanim przystąpimy do omówienia kwadratów hipermagicznych, musimy podać nieco wiadomości o liniach arytmetycznych.
Przypatrzmy się uważnie następnej tabelce; składa się ona z 9 kwadratów dwudzięstopięciopolowych, w które wpisane są kolejno liczby od 0 do 24.
Zamiast 9 kwadratów można by wziąć 16, 25, . . . kwadratów, można by również wziąć kwadraty nie 25-polowe, lecz z inną liczbą pól, bo chodzi tu właściwie nie o- ich ilość ani jakość, lecz o wytworzenie pewnego tła z ciągu liczbowego ułożonego w kwadraty, na którym to tle narysować będziemy mogli tak-zwane linie arytmetyczne i wyjaśnić ich znaczenie.
Bez użycia linijki i ołówka można dojrzeć od razu jedną z li ni j arytmetycznych, mianowicie przekątną biegnącą na przykład od pola zajętego przez 0 poprzez pole 6, dalej 12, 18, 24,. . .
Zauważymy tu zaraz pewną szczególną właściwość tej linii.
Szereg liczb, przez które biegnie linia arytmetyczna
0, 6, 12, 18, 24, …
można przedstawić w takiej postaci:
0, 1 + 5, 2 + 2 • 5, 3 + 3 • 5, 4 + 4 • 5, …
Jeśli więc pole wyjścia linii oznaczamy przez 0, to zawartość pierwszego przeciętego przez nią pola będzie 1 + wielokrotność 5, drugiego: 2 + wielokrotność 5, trzeciego: 3 + wielokrotność 5, czwartego: 4 + wielokrotność 5 i tak dalej.
Jeśli zamiast przeprowadzić w wyobraźni przekątną kwadratu, weźmiemy linijkę i ołówek i połączymy na przykład środek pola zajętego przez 0 ze środkiem pola zajętego w tymże kwadracie przez 16, to przekonamy się, że prosta, którą wykreślimy i przedłużymy dalej, przejdzie przez sam środek wielu
innych pól i utworzy się znów pewien ciąg liczb:
0, 16, 7, 23, 14, …,
który również napisać można tak:
0, 1 + 3 • 5, 2 + 1 • 5, 3 + 4 • 5, 4+2 • 5, …
Ponownie otrzymujemy więc to samo, co poprzednio, mianowicie: ciąg liczb wpisanych w pola, przez środki których biegnie owa linia arytmetyczna, składa się jakby z numerów porządkowych pól: 0, 1, 2, 3, 4, … plus pewne wielokrotności 5.
Takie to więc linie proste przechodzące przez środki szeregu pól nazywamy liniami arytmetycznymi. Przy figurach magicznych rozpatrywanych poprzednio mieliśmy do czynienia stale (bez użycia tej nazwy) z trzema rodzajami linij arytmetycznych, które w kwadratach magicznych były też liniami magicznymi, mianowicie z liniami poziomymi rzędów pól, liniami pionowymi kolumn i przekątnymi.
Obecnie więc rozszerzyliśmy tylko nasze zainteresowanie na inne linie ukośne, jakie wśród pól kwadratu można przeprowadzić, i nazwaliśmy wszystkie te linie mianem linij arytmetycznych.
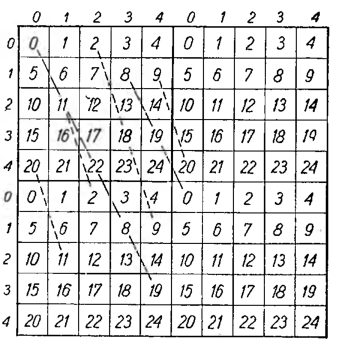Przyjrzyjmy się uważnie zamieszczonemu obok rysunkowi, na którym graficznie 0 przeprowadzone zostało kilka 1 arytmetycznych linij. Odległość między sąsiednimi środ- 3 kami pól leżących na linii 4 arytmetycznej nazywa się krokiem linii arytmetycznej.
Jeśli po brzegach prosto- 1 kąta ponumerujemy rzędy 2 pól i kolumny (jak to widzi- 3 my na rysunku), to każde 4 pole można oznaczyć numerami jako skrzyżowanie odpowiedniej kolumny i rzędu, stawiając zawsze na pierwszym miejscu numer kolumny, na drugim — numer rzędu. Na przykład na polu (2,3) znajduje się liczba 17, a na polu (3,2) — liczba 13.