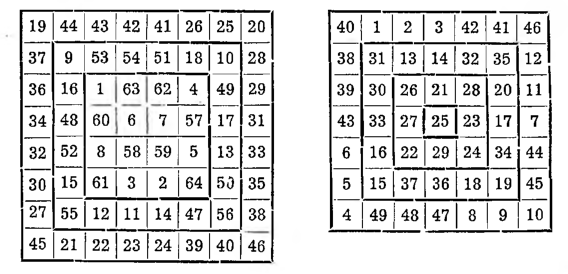
Kwadraty z obramowaniem. Są to kwadraty, które pozostają magiczne, chociaż odejmiemy jedno lub więcej z obramowań składających się z pól biegnących wzdłuż zewnętrznych rzędów i kolumn. Podany tu sposób budowy stosowany być może do wszelkich kwadratów i daje wielką ilość odmian.
Weźmy dla przykładu kwadrat magiczny rzędu szóstego i wytknijmy sobie za cel, by kwadrat miał jedno obramowanie, to znaczy, by kwadrat rzędu czwartego w nim zawarty pozostał magiczny po usunięciu obramowania.
Rozstawimy 36 pierwszych liczb w sposób następujący:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
36 35 34 33 32 31 30 29 28 27 26 25 24 23 22 21 20 19
Zbudujemy kwadrat rzędu czwartego z ośmiu jakichkolwiek liczb z linii pierwszej i ośmiu uzupełniających liczb z linii drugiej, na przykład:
1, 2, 3, 4, 5, 6, 7, 8 i 29, 30, 31, 32, 33, 34, 35, 36.
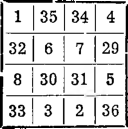Otrzymamy kwadrat z sumą magiczną 74. Kwadrat rzędu szóstego, który zamierzyliśmy zbudować, ma sumę magiczną, jak to już wiemy: 111. Stąd wniosek, że do każdej kolumny, do każdego rzędu i do każdej przekątnej powinniśmy dodać po dwie liczby, które w sumie dają 37 = 111 — 74; ale właśnie tę liczbę 37 dają wyżej wypisane liczby pierwszej i drugiej linii, gdy je będziemy parami sumowali. Bierzemy więc stojące jedna pod drugą liczby 9 i 28, 10 i 27 i ustawiamy je w rogach kwadratu (6 X 6) tak, by na przekątnych uzupełniały się wzajemnie do 37. Wiemy teraz, że w pierwszym rzędzie w czterech wolnych polach należy pomieścić liczby, które w sumie dadzą
111 — (9 + 10) = 92, w pierwszej zaś kolumnie suma liczb wstawianych powinna być 111 — (9 + 27) = 75.
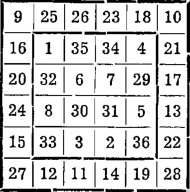Z liczb, które nam pozostały, mianowicie:
11 12 13 14 15 16 17 18
26 25 24 23 22 21 20 19
dla sumy 92 znajdziemy jako składniki na przykład liczby 26, 25, 23, 18. Ustawmy je w dowolnym porządku w pierwszym rzędzie, a w ostatnim rzędzie — ich dopełnienia. Wśród reszty liczb dobieramy dalej cztery składniki dające sumę 75, więc 16, 20, 24, 15 i umieszczamy je w pierwszej kolumnie, ich zaś dopełnienia — w ostatniej. W ten sposób otrzymamy pełny kwadrat magiczny rzędu szóstego z obramowaniem.
Jeszcze łatwiej zbudować można taki kwadrat, gdy do zestawienia kwadratu środkowego weźmiemy nie 8 pierwszych i 8 ostatnich liczb szeregu, lecz liczby środkowe:
11, 12, 18 i 19, …, 26.
Aby zbudować kwadrat rzędu ósmego, postępujemy zupełnie tak samo: budujemy kwadrat 4 X 4 i otaczamy go obramowaniem; otrzymawszy zaś kwadrat 6X6 znów go obramowujemy; dojdziemy wówczas do kwadratu 8X8.
Tę samą metodę stosować można do kwadratów nieparzystych. Jeślibyśmy chcieli np. zbudować kwadrat 7 X 7 z obramowaniem, to budujemy naprzód kwadrat 3X3, dodajemy doń obramowanie, otrzymamy kwadrat 5 X 5, a dodawszy drugie obramowanie osiągniemy poszukiwany kwadrat czterdziestodzie-więciopolowy.
