Zaprojektowana była wystawa. Dyrekcja rozpisała konkurs na godło wystawy.

Wśród, nadesłanych projektów znalazły się dwa pomysły o dość podobnych tematach.
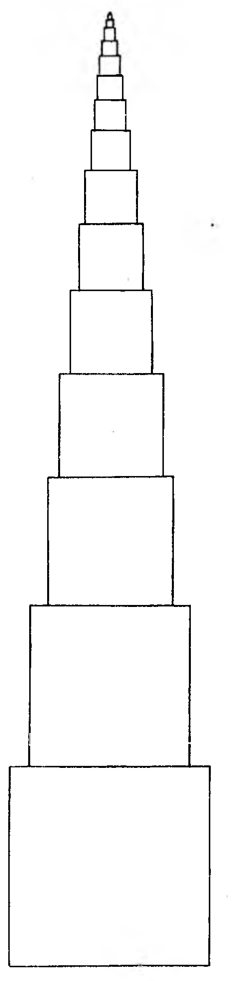
Jeden z tych projektów proponował, by godłem wystawy była piramida ze spiętrzonych sześcianów: na wielkim sześcianie o krawędzi a = 25 m ma być umieszczony sześcian o krawędzi o 20% mniejszej, na nim zaś nowy sześcian o krawędzi o 20% mniejszej od krawędzi poprzedniego sześcianu i tak dalej.
Drugi projekt kładł w podstawie piramidy sześcian o krawędzi a = 25 m, na nim miał być sześcian o krawędzi ½ a, potem z kolei sześciany o krawędziach 1/3 a,  1/4 a i tak dalej.

Która z tych piramid utworzonych z sześcianów będzie wyższa?

Okazuje się, że pierwsza wieża będzie miała 125 metrów wysokości. W samej rzeczy, trzeba obliczyć sumę szeregu geometrycznego

25 + 25 • 4/5 + 25 • (4/5)² + 25 • (4/5)³+ . . .

Jak wiadomo, suma taka wyraża się wzorem

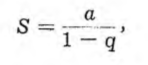gdzie a oznacza pierwszy wyraz szeregu, a  q — jego iloraz. W danym przypadku mamy a — 25, q = 4/5, a więc S = 125.

Dla obliczenia wysokości drugiej wieży trzeba znaleźć sumę takiego szeregu:

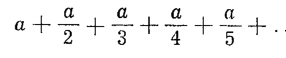Szereg taki nazywa się szeregiem harmonicznym. Otóż jest to szereg rozbieżny, gdyż suma jego wyrazów wziętych w dostatecznej ilości, może przekroczyć dowolnie wielką, z góry zadaną liczbę.

Łatwo to stwierdzić na podstawie nieco oryginalnego rozumowania. Wyrazy szeregu tego można połączyć w takie grupy:

stwierdzamy, że każdy nawias w pierwszym szeregu zawiera wyraz większy od odpowiedniego nawiasu w drugim szeregu. Ale drugi szereg jest rozbieżny, a więc i pierwszy szereg jest rozbieżny.

Widzimy więc, że wieżę według tego zaiste imponującego projektu trzeba by ciągnąć w górę w nieskończoność, ale po drodze doszlibyśmy do takiej wysokości, przy której siła odśrodkowa wskutek obrotu Ziemi dookoła osi byłaby większa niż siła przyciągania Ziemi.