Budowa parzysto-parzystych kwadratów magicznych

I.    Metoda La Hire’a. Powyżej przytoczona metoda z pewnymi modyfikacjami daje się zastosować do budowy kwadratów parzysto-parzystych. Pierwszy kwadrat pomocniczy wypełnia się wyrazami postępu 1, 2, 3, 4, ustawionymi w pierwszym wierszu w dowolnym porządku, z tym tylko zastrzeżeniem, żeby w całym kwadracie liczby dopełniające się, więc 1 i 4 oraz 2 i 3 rozmieszczone zostały w polach wzajemnie sobie odpowiadających, to znaczy leżących symetrycznie względem środka kwadratu; otrzymamy kwadrat magiczny z sumą 10.

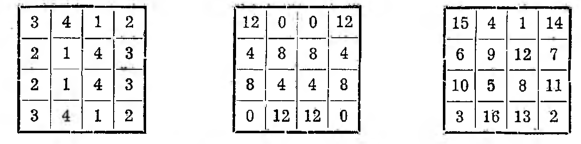Drugi kwadrat pomocniczy pomieści postęp 0, 4, 8, 12, to znaczy rozpoczynający się od ziera i złożony z kolejnych wielokrotności liczby podziałek boku. W pierwszej kolumnie tego kwadratu wpisuje się liczby w porządku dowolnym, w dalszych zaś kolumnach trzymać się należy tego samego, co wyżej, przepisu symetrii liczb. Otrzymujemy drugi kwadrat z sumą 24.

Z dodania liczb stojących w odpowiednich polach tych kwadratów tworzy się kwadrat trzeci z sumą magiczną 34.

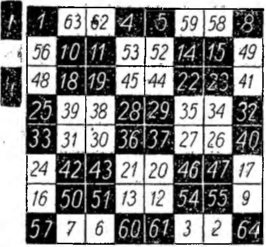
II.    Metoda Delanneya i Mondesira, Jest to metoda zupełnie nowoczesna, niezmiernie prosta, a zarazem pomysłowa, można powiedzieć wprost — dowcipna. Przedstawimy ją dla większej jasności na kwadracie — ósmego rzędu, to znaczy 64-poloWym, ale stosować ją można równie dobrze i do kwadratów 16-poloWych. Należy na kwadracie tym przez zaczernienie pewnych pól, jak wskazano na rysunku, utworzyć rodzaj szachownicy.

Uważne rozpatrzenie się w podanym tu przykładzie rzecz dostatecznie wyjaśnia. Otrzymany kwadrat ma sumę magiczną 260.