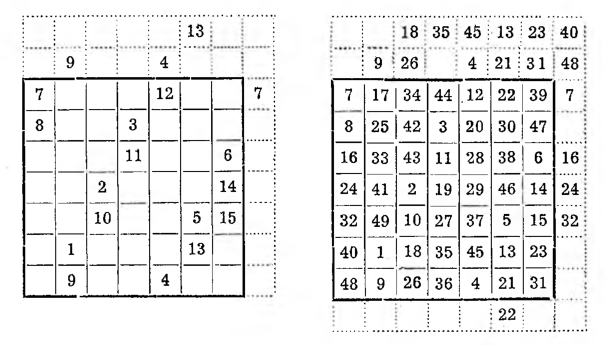
IV.    Metoda La Louber’a. Pokażemy ją na kwadracie rzędu piątego. Zamiast piramidek dobudowuje się do kwadratu głównego cztery inne kwadraty tejże wielkości, przez co otrzymuje się figurę podaną obok.

W środkowym polu lewej kolumny wpisujemy 1 i idąc na ukos na prawo ku górze wpisujemy liczby 2, 3, 4, 5.

Po wpisaniu pierwszej piątki zatrzymujemy się.

Liczby 4 i 5 wyszły poza ramki kwadratu. Gdy każdą z nich przesuniemy o 5 pól w dół, wówczas znajdą się one wewnątrz kwadratu (obacz gotowy kwadrat na następnej figurze).

Pod tym nowym położeniem liczby 5 wpisujemy 6 i znowu idąc na prawo ku. górze wpisujemy 7, 8, 9, 10, Po wpisaniu drugiej piątki widzimy, że liczby 7, 8, 9, 10 wyszły poza ramki kwadratu; wprowadzamy je do kwadratu za pomocą przesunięcia o 5 pól w lewo. Pod nowym położeniem liczby 10 wpisujemy 11 i dalej 12, 13, 14, 15.

Aby umieścić w kwadracie liczby 13, 14, 15, trzeba będzie przesunąć je o 5 pól w dół i o 5 pól na lewo. Tak postępujemy do końca.

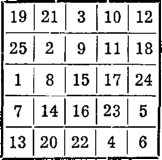Gdy dojdziemy do ostatniego wyrazu postępu, czyli, jak w danym razie, do 25, wówczas wszystkie liczby stojące w kwadratach dodatkowych przenosi się na analogiczne pole kwadratu głównego i otrzymuje się kwadrat magiczny odmienny od poprzedniego, otrzymanego metodą Bacheta. Pod polem 25 będzie pole 1.

V.    Pewna odmiana poprzedniej metody. Natchnieni myślą La L o u b e r e’a podajemy pewną odmianę jego metody dającą symetryczne kwadraty magiczne rzędu piątego. Otóż wypisujemy na papierze kratkowanym ciąg liczb tak rozmieszczony;

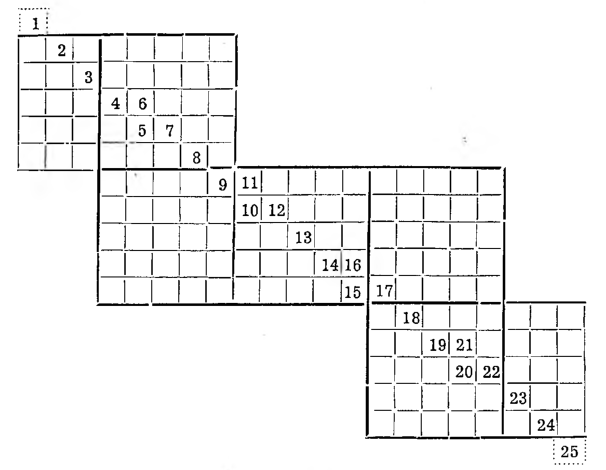Po wpisaniu wszystkich liczb do kratek wykreślamy grubszymi kreskami taki kwadrat, ażeby na jego przekątnej leżały liczby grupy podstawowej: 11, 12, 13, 14, 15, a następnie — w dostosowaniu do tego kwadratu — kreślimy grubszymi kreskami inne kwadraty rzędu piątego lub ich części.

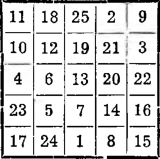Teraz już nie trudno będzie przesunąć wszystkie liczby do wnętrza kwadratu głównego i otrzymać poszukiwany kwadrat magiczny. Jest to, jak łatwo stwierdzić, symetryczny kwadrat magiczny.

Kwadraty symetryczne mają ciekawą własność oryginalnego przeistaczania się w kwadraty innego typu. Mo^na mianowicie przesunąć drugi rząd liczb o jedną kratkę na prawo, potem trzeci rząd o dwie kratki na prawo i tak dalej, a następnie cały trójkąt wysuniętych liczb przerzucić do pustych kratek na lewo, jak to wskazuje schemat:

Otrzymaliśmy znowu kwadrat magiczny, ale już niesymetryczny.

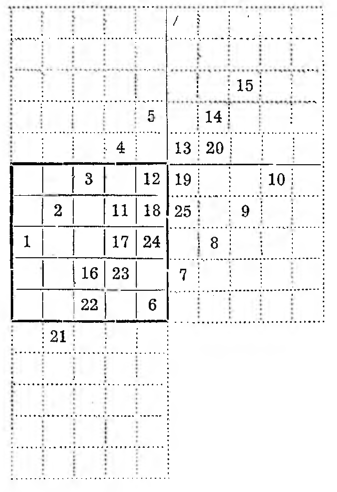
VI.    Metoda skoków konika szachowego, bardzo oryginalna, a zarazem łatwa i ciekawa. Weźmiemy tym razem dla przykładu znów kwadrat rzędu siódmego, czyli czterdziestodziewięciopolowy. Jedynkę stawiamy w którymkolwiek polu, nad nią zaś 2, 3 i tak dalej wpisujemy w polach, na które wypadłby skok konika szachowego. Czwórka wyjdzie już poza obręb kwadratu, należy więc ją przenieść na pole analogiczne wewnątrz kwadratu i dalej od niej kontynuować skoki. Gdy dojdziemy do siódemki, a potem do dalszych wielokrotności 7, to znaczy do 14, 21, . . ., liczbę następną, tj. 8, 15, 22, . . . podpisujemy w polu bezpośrednio niższym i od niej znów skokami konika rozstawiamy dalsze liczby, dopóki nie dojdziemy do 49.