Pewna firma ma odbiorców na parterze i na każdym piętrze sześciopiętrowego budynku. Schody pomiędzy poszczególnymi piętrami mają po 18 stopni, a przed drzwiami wejściowymi znajduje się jeszcze podmurek z 6 stopni.

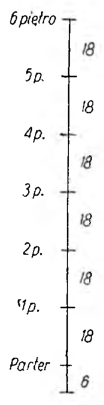Któregoś dnia posłaniec musiał dostarczyć każdemu z klientów jednakowej wielkości paczki, przy czym za każdym razem mógł unieść tylko jedną paczkę. Po ilu stopniach będzie musiał wejść i zejść, by dostarczyć wszystkie paczki do miejsca ich przeznaczenia?

Aby zanieść pierwszą paczkę na parter, posłaniec wejdzie 6 stopni; aby odnieść drugą na I piętro, 6 + 18 stopni; aby odnieść trzecią na II piętro, 6 + 2 • 18 stopni; . .. wreszcie aby odnieść siódmą paczkę na VI piętro, 6 + 6 • 18 = 114 stopni.

Posłaniec wchodzi więc na taką ilość stopni, jaką będzie suma postępu arytmetycznego złożonego z 7 wyrazów, którego pierwszy wyraz jest 6, a różnica 18.

Sumę tę obliczamy według wzoru

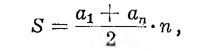gdzie n oznacza liczbę wyrazów postępu, a1 — pierwszy wyraz postępu, an — ostatni wyraz. Otrzymamy

S = [(6+114)/2] • 7 = 420 stopni

Schodzić będzie tę samą ilość stopni, czyli ogółem będzie musiał przebyć 2 • 420 = 840 stopni. Wliczyliśmy do tej liczby stopnie, z których posłaniec musiał zejść po zaniesieniu ostatniej paczki na VI piętro.

Jak to nieraz bywa w brzmieniu zadań rozrywkowych, może tu zajść pewna dwoistość interpretacji. Oto gdy posłaniec „dostarczył paczki do miejsca ich przeznaczenia”, sam znalazł się na wysokości VI piętra .. ., a więc — ściśle mówiąc — w tym momencie wszedł i zeszedł 840 — 114 = 726 stopni. Gdy więc ktoś obliczy, że posłaniec musiał przejść 840 stopni, można temu zaprzeczyć „w imię ścisłości”.