 W pewnej odległości od szosy, biegnącej w tym miejscu po linii prostej, leżą dwie wioski. Szosą przejeżdża poczta. Sołtysi umówili się, że jednego dnia jeden, drugiego dnia drugi będą wysyłali posłańca; posłaniec zaś odbierze pocztę i naprzód odniesie do sąsiada listy, które poczta dlań przyniosła, a następnie z resztą korespondencji powróci do swej wsi.
W pewnej odległości od szosy, biegnącej w tym miejscu po linii prostej, leżą dwie wioski. Szosą przejeżdża poczta. Sołtysi umówili się, że jednego dnia jeden, drugiego dnia drugi będą wysyłali posłańca; posłaniec zaś odbierze pocztę i naprzód odniesie do sąsiada listy, które poczta dlań przyniosła, a następnie z resztą korespondencji powróci do swej wsi.
W którym miejscu szosy powinien znaleźć się posłaniec, aby odbyć najkrótszą drogę przy tych peregrynacjach?
Jest to zagadnienie nie bez znaczenia, gdyż jeślibyśmy przypuścili, że posłaniec nakłada niepotrzebnie choć tylko 100 metrów drogi dziennie, drobna ta nieścisłość w ciągu roku uczyniłaby 36½ kilometra zbytecznej fatygi, zdzierania podeszew i straty czasu.
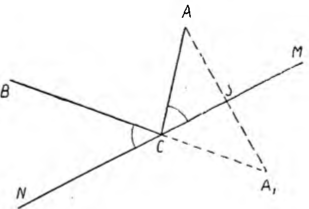 Jeśli szosę oznaczymy linią MN, a wsie punktami A i B, to dla odnalezienia poszukiwanego punktu na szosie należy z punktu A przeprowadzić prostopadłą do MN i od punktu przecięcia S odłożyć SA1=SA, następnie połączyć linią prostą B z A1. Wówczas przecięcie tej linii z szosą da poszukiwany punkt C.
Jeśli szosę oznaczymy linią MN, a wsie punktami A i B, to dla odnalezienia poszukiwanego punktu na szosie należy z punktu A przeprowadzić prostopadłą do MN i od punktu przecięcia S odłożyć SA1=SA, następnie połączyć linią prostą B z A1. Wówczas przecięcie tej linii z szosą da poszukiwany punkt C.
Obrazowo można by to przedstawić, jak następuje: wyobraźmy sobie, że wzdłuż szosy ustawione jest olbrzymie zwierciadło zwrócone w stronę wsi. Wówczas posłaniec wychodzący z B powinien się kierować w prostej linii ku odbiciu wsi A w lustrze — i odwrotnie: posłaniec z A powinien iść ku B widzianemu w zwierciadle. Wówczas obaj osiągną ów poszukiwany punkt C.