Słynny był podobno niegdyś we Francji pewien znakomity kawalerzysta, który bez względu na liczbę uczestników wesołych kawalkad potrafił momentalnie odpowiedzieć, ilu różnymi sposobami mogli się jeźdźcy ugrupować w równe szeregi, jadąc po dwóch, pc trzech, po czterech, przy czym w żadnym szeregu jeźdźca nie brakło i nikt nie zbywał.
Zjeżdżało się w tych czasach nieraz po kilkadziesiąt i parę-set osób rycerzy i dam, a nie zdarzyło się, by ów rachmistrz w swym orzeczeniu kiedykolwiek się pomylił.
Wezwał go kiedyś król w czasie defilady licznych zastępów wojskowych i rzekł:
—    W tym oddziale jest 1260 ludzi. Ilu sposobami można ich ustawić w równych szeregach?
—    Na 34 sposoby, miłościwy panie.
—    A w tamtym 7560? …
Zadanie było trudniejsze nieco, więc kawaler dłuższą chwilę pomyślał, ale wnet już miał odpowiedź gotową: na 62 sposoby!
—    Jakże to robicie, panie kawalerze?
—    Och, nic łatwiejszego: każdy z wykładników potęg podzielników będących liczbami pierwszymi powiększam o jedność, mnożę i odejmuję dwójkę, bo wszak niesposób jechać gęsiego lub wszyscy w jednym szeregu.
Usłyszawszy takie objaśnienie król podobno zbladł i zaniechał dalszej indagacji, gdyż poczuł, że go zamroczyło, a nie chciał dać tego po sobie poznać. Pożegnał tedy grzecznie kawalera i odjechał ze swą świtą czym prędzej, nie zważając, czy jadą „gęsiego”, czy wszyscy w jednym szeregu . ..
Szybkie odnajdywanie liczby podzielników, które w owych czasach mogło się wydawać czymś fenomenalnym, jest dziś dostępne — przy pewnej wprawie — wielu wcale nie fenomenalnym rachmistrzom.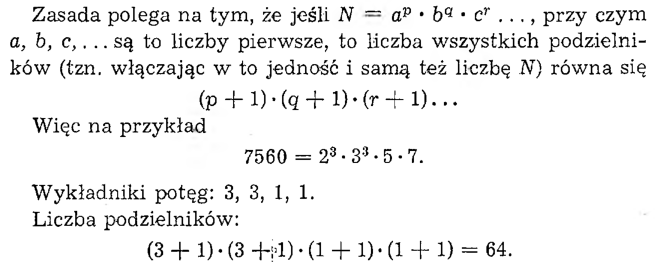Ów fenomenalny kawalerzysta wyłączał jednak jazdę „gęsiego” i w jednym szeregu, dlatego odpowiedź jego brzmiała 62.