Dwóch ogrodników spierało się o ilość wody znajdującej się w beczce; chodziło o rozpuszczenie w niej soli potasowej. Jeden z nich twierdził, że w beczce jest wody więcej niż połowa, drugi obstawał, że jest mniej. Jak się przekonać, kto ma rację, nie używając ani patyka, ani sznurka, ani niczego, co by mogło służyć do pomiaru?

Oto wyjaśnienie:
Mamy przed sobą nie żart matematyczny, lecz prawdziwe zadanie geometryczne, chociaż rozwiązanie jest śmiesznie łatwe.
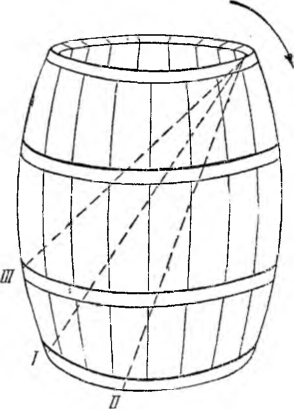
Jeśliby beczka była istotnie równo do połowy napełniona wodą, to nachyliwszy beczkę tak, żeby powierzchnia wody dosięgła jej brzegu, zobaczylibyśmy, że wyższy punkt dna znajduje się również na powierzchni wody (poziom I na rysunku). Wynika to z tego, że płaszczyzna przeprowadzona przez diametralnie przeciwległe punkty górnego i dolnego obwodu beczki dzieli ją na dwie równe części.

Jeśli wody jest mniej niż połowa beczki, to przy takim pochyleniu musi wystąpić z wody mniejszy lub większy odcinek dna (poziom II).

Wreszcie jeśli wody jest więcej niż połowa beczki, to przy pochyleniu całe dno będzie pod wodą (poziom III).

W ten sposób bez jakichkolwiek pomiarów mamy dokładną odpowiedź.