Dziewięć cyfr od 1 do 9 wypisano na dziewięciu kartkach i rozdano trzem osobom. Każda osoba ułożyła z otrzymanych trzech kart liczbę trzycyfrową możliwie najmniejszą, to znaczy, iż na miejscu setek postawiła najniższą posiadaną cyfrę, na miejscu dziesiątek — wyższą, a na miejscu jedności — najwyższą. Po ułożeniu owych liczb wszystkie trzy osoby odczytały je głośno i zapisały. Okazało się wówczas, że suma cyfr wszystkich trzech liczb była dziwnym trafem jednakowa. Zmieszano potem kartki i ponownie rozdano po trzy. Każdy z uczestników tej zabawy otrzymał przypadkowo jedną z kart poprzednio posiadanych i dwie nowe. I znowu dziwnym zaiste trafem sumy cyfr były jednakowe, a co jeszcze ciekawsze, u każdej z osób liczba ułożona poprzednio i liczba ułożona obecnie dawały tę samą sumę 516.
Jakie cyfry otrzymał każdy przy pierwszym i drugim rozdaniu?
Suma pierwszych dziewięciu liczb 1 + 2 + 3 + .. . + 9 = 45. Więc suma cyfr przy pierwszym i drugim rozdaniu u każdego z obecnych musiała wynosić 15. Na miejscu jedności w poszukiwanych liczbach nie mogły stać cyfry 1, 2, 3, 4 ani 5, gdyż wówczas nawet największa liczba trzycyfrowa, jaką by można według podanych zasad ułożyć (345), daje w sumie cyfr 12.
Suma liczb (516) kończy się na 6, więc jedności w liczbach sumowanych musiały być reprezentowane przez 7 i 9 albo przez 8 i 8. Dla dziesiątek i setek zostały cyfry od 1 do 6.
Lecz 7 + 9 = 8 + 8 = 16; 516 — 16 = 500. Poszukiwana więc przez nas suma dziesiątek daje 0, to znaczy, że na drugim miejscu musiały stać cyfry 4 i 6 albo 5 i 5. Suma setek wobec tego równa się 4, więc na miejscu setek stały 1 i 3 albo 2 i 2.
U każdej osoby w obu liczbach powtarzała się jedna cyfra: jeżeli powtórzyła się 8, to dziesiątkami mogły być tylko 4 i 6, a setkami 3 i 1; stąd liczby: 348 i 168. Jeśli u drugiej osoby powtórzyła się 5, to jednościami mogły być tylko 7 i 9, a setkami 1 i 3; stąd liczby 159 i 357. U trzeciej osoby powtórzyła się 2, dziesiątkami były więc 4 i 6, jednościami 9 i 7; były więc liczby: 267 i 249.
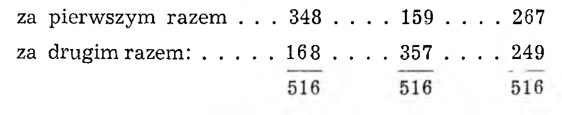
Zróbmy zestawienie liczb:
