Aby oznaczyć krok linii, wystarczy wypisać dwa najbliższe sobie pola, przez środki których biegnie linia, więc na przykład (2,0) i (3,3).
Na podstawie tej numeracji możemy nie patrząc zgoła na rysunek wypisać dalszy szereg pól, przez środki których przejdzie linia tym krokiem idąca. Wystarczy do numeru kolumny (tj. liczby stojącej w nawiasie na miejscu pierwszym) dodawać stale po 1 = (3 — 2), a do numeru rzędu dodawać wciąż po 3 = (3 — 0); otrzymamy wówczas pola takie:
(2,0), (3,3), (4,6), (5,9), (6,12), (7,15),…
Części linii wychodzące poza ramy pierwszego kwadratu możemy zawsze sprowadzić do kroków analogicznych w tymże kwadracie. Na przykład nakreślmy linię (0,0) — (1,2); przejdzie ona dalej przez pola (2,4), (3,6), (4,8) i tak dalej. Otóż odcinek tej linii, mianowicie jej krok (3,6) — (4,8), sprowadzić można do kroku (3,1) — (4,3).
Jeśli punktem wyjścia linii jest środek pola (0,0), to chcąc określić czwarte pole przy kroku (1,3), wystarczy wziąć pole o numerach 4 • 1 i 4 • 3, co w skróceniu oznaczyć można:
4 • (1,3), a więc przy tych warunkach zamiast ciągu (0,0), (1,3), (2,6), (3,9), (4,12), (5,15), .. ., można wypisać ciąg taki:
(0,0), (1,3), 2 -(1,3), 3 -(1,3), 4 .(1,3), 5 .(1.3),…
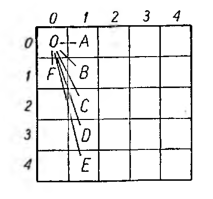 Wśród wielkiej ilości linij arytmetycznych, które można przeprowadzić z rozmaitych pół we wszystkich kierunkach, wyróżniamy tak zwane główne linie arytmetyczne, oznaczone na poniższym rysunku. Wychodzą one wszystkie z pola (0,0), a kroki ich są następujące:
Wśród wielkiej ilości linij arytmetycznych, które można przeprowadzić z rozmaitych pół we wszystkich kierunkach, wyróżniamy tak zwane główne linie arytmetyczne, oznaczone na poniższym rysunku. Wychodzą one wszystkie z pola (0,0), a kroki ich są następujące:
krok (1,0) czyli OA
„ (1,1) ,, OB
„ (1,2) „ OC
„ (1,3) „ OD
„ (1,4) „ OE
oraz krok (0,1) „ OF
Ilość linij głównych dla kwadratu 25-polowego wynosić będzie 6, to znaczy 5 + 1, a w ogóle: n + 1, jeśli n jest liczbą pól w rzędzie lub kolumnie kwadratu.
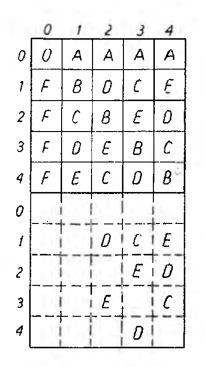 Główne linie arytmetyczne przejdą przez następujące pola (po sprowadzeniu ich dalszych odcinków w drugim kwadracie do analogicznych kroków w głównym kwadracie):
Główne linie arytmetyczne przejdą przez następujące pola (po sprowadzeniu ich dalszych odcinków w drugim kwadracie do analogicznych kroków w głównym kwadracie):
Linia OA : (0,0), (1,0), (2,0), (3,0), (4,0)
„ OB : (0,0), (1,1), (2,2), (3,3), (4,4)
„ OC : (0,0), (1,2), (2,4), (3,1), (4,3)
„ OD: (0,0), (1,3), (2,1), (3,4), (4,2)
„ OE: (0,0), (1,4), (2,3), (3,2), (4,1)
„ OF : (0,0), (0,1), (0,2), (0,3), (0,4)
Z zestawienia tego widzimy, iż każde pole głównego kwadratu będzie stanowiło punkt krańcowy kroków pewnej linii głównej, przy czym tylko pole (0,0) będzie wspólne wszystkim liniom, w żadnym natomiast innym polu linie główne się nie spotykają.
Ograniczymy się tu do wskazania powyższych kilku właściwości linij arytmetycznych, potrzebnych do zrozumienia kwadratów hipermagicznych, zachęcając gorąco Czytelników do samodzielnego odszukiwania wielu innych ciekawych znamion. Może natrafią przy tym na rzeczywiste „odkrycia”, a jeśli nawet zdobędą tylko rzeczy już znane, przez poprzedników wykryte i zapisane w teorii owych linij, zawszeć skorzystają na wygimnastykowaniu swej spostrzegawczości, zmysłu orientacyjnego i kombinacyjnego.