Budowa nieparzystych kwadratów magicznych

Różnych metod budowy kwadratów magicznych jest bardzo wiele. Wśród nich najwięcej jest przepisów na zestawianie kwadratów nieparzystych, najmniej dla kwadratów nieparzysto-parzystych. Przytoczone poniżej prawidła są względnie najłatwiejsze, a zarazem najciekawsze.

Podajemy ogólne tylko zarysy tych metod, umyślnie ich nie precyzując, aby Czytelnik mógł, samodzielnie je przerabiając według własnej inicjatywy, odnaleźć nowe a interesujące ich odmiany.

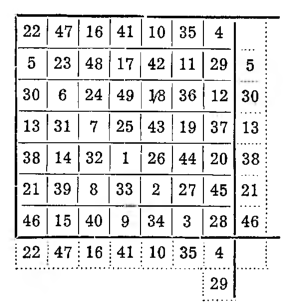I.    Metoda hinduska przekazana matematykom europejskim przez wspomnianego wyżej Moscopulosa. Dla przykładu weźmy kwadrat siódmego rzędu, to znaczy 49-polowy. Stawiamy jedynkę w polu znajdującym się bezpośrednio pod polem środkowym i od niej piszemy ku prawej stronie w dół po przekątnej dalsze wyrazy naturalnego ciągu liczb.
Czwórka wypadnie już poza kwadratem; przenosimy ją w analogiczne pole wewnątrz kwadratu.
Piątka znów wyjdzie poza kwadrat; postępujemy z nią tak samo, jak z czwórką. Doszedłszy do 7 napotykamy na drodze pole zajęte już przez jedynkę. W tym przypadku stawiamy 8 pod 7 o dwa pola niżej i kontynuujemy na tych samych zasadach wypisywanie liczb dalszych aż do 49. Otrzymamy w rezultacie kwadrat z sumą magiczną 175.
Warto przerobić tę metodę na kwadracie innego rzędu stawiając 1 zamiast pod środkowym polem — nad tym polem i posuwając się w odmiennym kierunku po przekątnych.

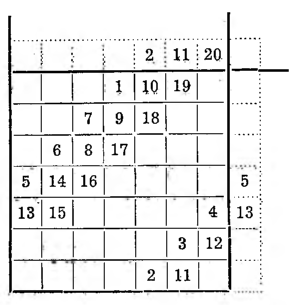II. Metoda syjamska. Podaje ją La Loubere w swym dziele pod tytułem Du royaume de Siam; był on posłem Ludwika XIV do króla Syjamu (1687—1688) i tam się z tą metodą zapoznał.

Pierwszy wyraz postępu stawia się w środkowym polu górnego rzędu i wpisuje się dalsze wyrazy w kierunku na prawo ku górze postępując tak, jak w metodzie poprzedniej, z tą tylko różnicą, iż doszedłszy np. siódemką do pola zajętego wpisuje się 8 nie o dwa pola niżej, lecz bezpośrednio pod siódemką.
I tę metodę zaleca się wypróbować na innych kwadratach umieszczając 1 nie w górnym, lecz w dolnym rzędzie.

III.    Metoda Bach et a, jedna z najpiękniejszych i najprostszych. Polega ona na dobudowaniu do kwadratu czterech pomocniczych piramidek z wszystkich czterech jego stron, jak to widać na załączonym tu przykładzie kwadratu o 25 polach.

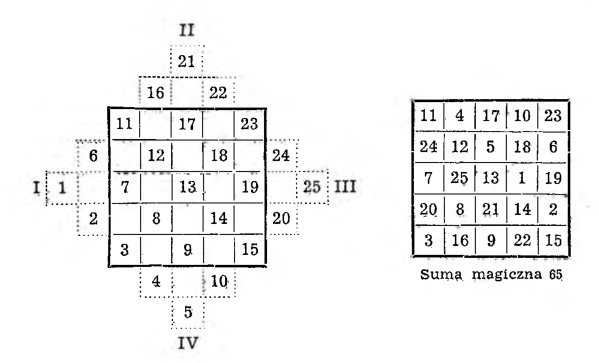Rozpoczynając następnie z któregokolwiek wierzchołka jednej piramidki i idąc po linii równoległej do przekątnej kwadratu, wpisuje się kolejno wszystkie 25 liczb, po czym liczby będące poza bokami kwadratu przenosi się do jego wnętrza w ten sposób, że piramidkę I wpisuje się dookoła 19, piramidkę II dookoła 9 i tak dalej.

W rezultacie otrzymuje się kwadrat magiczny z sumą 65.

Jest to kwadrat symetryczny. Wzdłuż jednej z przekątnych pięknie układa się postęp: 11, 12, 13, 14, 15 — ze szczęśliwą trzynastką pośrodku, a każda para liczb symetrycznych względem środka daje w sumie 26, czyli 2 • 13.