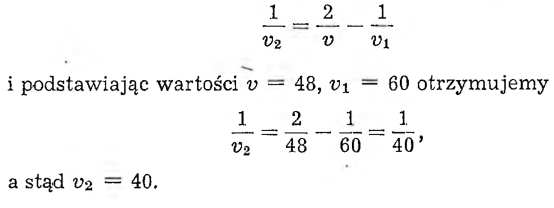Automobilista brał udział w konkursie jazdy regularnej. Według regulaminu powinien przejechać pewien odcinek drogi z przeciętną prędkością 48 km na godzinę. Tymczasem połowę drogi gnał z prędkością 60 km na godzinę. Do jakiej liczby musi obniżyć prędkość jazdy na drugiej połowie drogi, aby średnia prędkość spadła do 48 km na godzinę?

Jeśli sądzisz, że drugą połowę drogi będzie musiał automobilista wlec się z prędkością 36 km na godzinę, to się mylisz,
chociaż (60+36)/2 = 48.

Przypuśćmy, że cała droga wynosiła 120 km. Na jazdę konkursową automobilista ma preliminowane 120 : 48 = 2½ godziny— ani mniej, ani więcej. Skoro więc pierwszą połowę drogi, czyli 60 km, przejechał w ciągu godziny, to na drugą połowę drogi zostało mu 1½ godziny, a więc musiał jechać z prędkością 60 : 1½ = 40 km na godzinę.

Rozważmy sprawę ogólniej. Przypuśćmy, że długość całej drogi wynosiła 2d i że automobilista przejechał pierwszą połowę drogi z prędkością v1, a drugą połowę z prędkością v2. Obliczmy, jaka była przeciętna prędkość v jazdy na całej drodze.
Na pierwszą połowę drogi automobilista zużył czas d/v1 , a na drugą połowę d/v2, więc na całą drogę zużył czas d/v1 + d/v2.

Z drugiej strony, na drogę 2d przy prędkości jazdy v potrzeba czasu 2d/v.

Otrzymujemy równanie

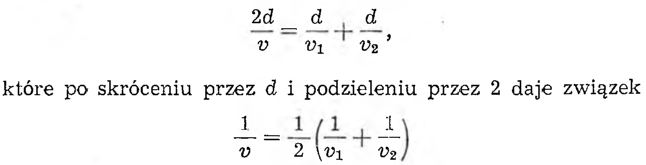Okazuje się, że odwrotność prędkości v jest średnią arytmetyczną między odwrotnościami prędkości v1 i v2. Mówimy w takim przypadku, że prędkość v jest średnią harmoniczną między prędkościami v1 i v2.

W naszym zadaniu mamy dane v = 48 i v1 = 60, a trzeba wyznaczyć v2.

Z powyższego równania obliczamy